История развития геометрии

Краткая биография

Биография Евклида до конца не изучена, к примеру, до сих пор неизвестен год рождения. Известно, что он появился на свет в небольшом районе Афин и был платоновским учеником.

Подъем его научной работы пришелся на правление Птолемея Первого. Некоторые сведения о его жизни можно проследить по арабским рукописям и архимедовым письмам к друзьям. Так, по ним можно определить, что Евклид был сыном греческого ученого и жил около Тира в Сирии.

С малых лет получал знания о мире от своего отца, он же привил сыну любовь к естественным наукам, а затем Евклид поступил в школу Платона, где и обучился математическим основам.

Повзрослев, его пригласили в храм Мусейон (по другим данным он был одним из его основателей), в котором собирались видные ученые с поэтами. Тут были классы для занятий. Также храм был заполнен садами с башнями астрономии, помещениями для одиноких размышлений и большой библиотекой.

В Мусейоне он смог открыть школу с лучшими математиками и монументальный труд в области математики, в котором заложил планиметрические основы со стереометрией, теорией чисел, законами алгебры, методами нахождения площадей с объемами и др.

Фрагмент папируса с текстом «Начал» Евклида

Монументальный труд — публикация «Начала». Это серия из 13 книг, представляющая собой обработанные публикации древнегреческих математиков с пятого по четвертый век до нашей эры.

Кроме «Начал», было создано еще одно сочинение — «Данные», в котором были опубликованы основы по геометрическому анализу. Кроме того, александрийский ученый создал учебник, с помощью которого в то время и сейчас изучают астрономию, перспективу, отражение в зеркале, музыкальные интервалы и решают тригонометрические задачи.

Все оставшиеся годы жизни посвятил изучению естественных наук и математических законов, отчего его называют отцом геометрии. О других аспектах его жизни неизвестно до сих пор. Умер в Александрии.

Это интересно: 231,ДУХОВНАЯ КУЛЬТУРА — разбираемся внимательно

XVIII — го века

Г. Саккери — Псевда демонстрация V — й аксиома эксгумировано из забвения истории поддерживающего Beltrami , один из основателей современной дифференциальной геометрии.

XVIII — го  век не сравним с прошлым веком , чтобы рассматривать геометрию. Это период перехода и углубления.

Два величайших математиков века, Эйлера и Лагранжа замечательные геодезисты, а также способствовать развитию евклидовой геометрии (например , углы Эйлера , Эйлера линии , окружности Эйлера …).

Тем не менее, основные изменения геометрии в XVIII — го  века, связаны с тем , механики и связаны с дифференциальной геометрией. Это уточнения идей Лейбница и Ньютона. Клеро ( Исследования кривых двойной кривизны — 1732) изучает уравнения кривых в пространстве, которые теперь называются левыми кривыми. В 1760 году Эйлер опубликовал свое « Исследование кривизны поверхностей» , в котором он показал существование двух основных искривлений и продемонстрировал то, что сейчас называется теоремой Эйлера . Уважаемые ученые, такие как Мёзье или Дюпен, также внесли интересный вклад в фундаментальную работу Эйлера по геометрии поверхностей. Выявлены важные понятия длины дуги кривой, соприкасающейся окружности . Дифференциальные выражения кривизны и кручения левой кривой дается Коши в начале XIX — го  века.

Кроме того, Лежандр опубликовал в 1794 году « Элементы геометрии», которые составляют один из последних великих трактатов по евклидовой геометрии . К несчастью для него, этот ученый верит в доказуемость пятой аксиомы Евклида и дает несколько доказательств, которые, конечно, ложны, хотя и обладают замечательным интеллектом … Основы геометрии, в том числе 5- я  аксиома Евклида, продолжают вдохновлять некоторые математики, такие как Ламберт или Саккери .

К концу века Монж создал особую ветвь геометрии, называемую начертательной геометрией , которая была направлена ​​на то, чтобы помочь инженеру в представлении машин. Правила , разработанные Монжем широко используются на протяжении XIX — го  века , и большая часть XX — го . Они составят теоретическую основу практики промышленного дизайна .

После работы XVII — го и XVIII — го  века геометрия Евклида достигла своего наибольшего развития, но знаменитые геометрические проблемы , унаследованных от античности до сих пор не решены, хотя почти ясно для большинства ученых , что они представляют собой невозможные проблемы, к тому , что с 1775 г. Академия наук решает отказать в рассмотрении адресованных ей предложений квадрата круга.

В конце 18 века мы можем все чаще различать две разные геометрии: геометрия Евклида, который рассуждает о фигурах, называется синтетической геометрией . Геометрические рассуждения в духе Декарта о числах и функциях чисел называются аналитической геометрией. Однако нет никаких сомнений в идентичности материалов, даже если методы различны.

Евклид.

В III в. до н. э. древнегреческий ученый Евклид написал книгу под названием «Начала». В этой книге Евклид подытожил накопленные к тому времени геометрические знания и попытался дать законченное аксиоматическое изложение этой науки. Написана она была настолько хорошо, что в течение 2000 лет всюду преподавание геометрии велось либо по переводам, либо по незначительным переработкам книги Евклида.
Продуманное и глубоко логическое изложение геометрии, данное в книге Евклида, привело к тому, что математики не мыслили возможности существования геометрии, отличной от евклидовой. Лишь в XIX в. благодаря в первую очередь трудам выдающегося русского математика Н. И. Лобачевского было установлено, что евклидова геометрия не является единственно возможной.
Часто идеи, обогащающие математику новыми понятиями и методами, приходят из физики, химии и других разделов естествознания. Типичным примером может служить понятие вектора пришедшее в математику из механики. В отношении неевклидовых геометрий обстоит как раз наоборот: созданные внутри математики эти новые геометрические понятия положили пути создания современной физики.

Много нового появилось со времен Евклида и в самой евклидовой геометрии. Еще в XVII в. благодаря работам французского математика и философа Р. Декарта возник метод координат, ознаменовавший собой революционную перестройку всей математики, и в частности геометрии. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так в рамках евклидовой геометрии появилась ее новая ветвь — аналитическая геометрия.
В работах математиков XIX в. У. Гамильтона, Г. Грассмана и других были введены векторы, которые ранее в трудах Архимеда, Г. Галилея и других имели лишь механический смысл, а теперь приобрели права в математике.
Другим важным обогащением, которым геометрия также обязана XIX в., стало создание теории геометрических преобразований, и в частности движений (перемещений). У Евклида движения неявно присутствовали; например, когда он говорил: «Наложим один треугольник на другой таким-то образом», то речь шла в действительности о применении движения, перемещения треугольника.

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Все эти фигуры обладают двумя свойствами:

• симметрия
• равенство или подобие составных частей.

Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.

У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.

Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).

Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.

Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.

Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.

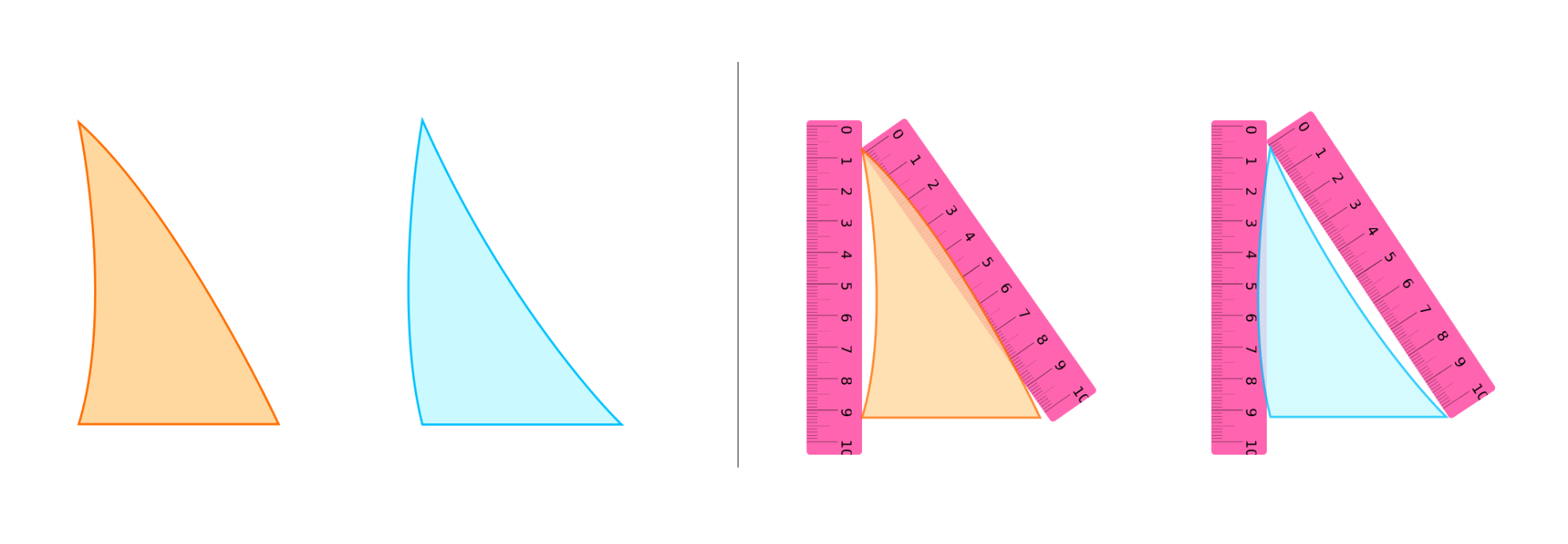
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.

Псевдо-Евклид

Евклиду приписываются два важных трактата об античной теории музыки: «Гармоническое введение» («Гармоника») и «Деление канона» (лат. Sectio canonis). Традиция приписывать «Деление канона» Евклиду идёт ещё от Порфирия. В старинных рукописях «Гармоники» авторство приписывается Евклиду, некоему Клеониду, а также александрийскому математику Паппу. Генрих Мейбомrude (1555—1625) снабдил «Гармоническое введение» обстоятельными примечаниями, и вместе с «Делением канона» приписал их к трудам Евклида.

При последующем подробном анализе этих трактатов было определено, что первый написан в аристоксеновской традиции (например, в нём все полутоны считаются равными), а второй по стилю — явно пифагорейский (например, отрицается возможность деления тона ровно пополам). Стиль изложения «Гармонического введения» отличается догматизмом и непрерывностью, стиль «Деления канона» несколько схож с «Началами» Евклида, поскольку содержит теоремы и доказательства.

После критической публикации «Гармоники» знаменитым немецким филологом Карлом Яном (1836—1899) этот трактат стали повсеместно приписывать Клеониду и датировать II в. н.э. В русском переводе (с комментариями) его впервые издал Г. А. Иванов (Москве, 1894). «Деление канона» ныне одна часть исследователей считает аутентичным сочинением Евклида, а другая — анонимным сочинением в традициях Евклида. Последние по времени русские переводы «Деления канона» опубликованы (в версии Порфирия) В.Г.Цыпиным и (в версии Боэция) С.Н.Лебедевым. Критическое издание оригинального текста «Деления канона» выполнил в 1991 г. А.Барбера.

• Назад

• Вперёд

Добавить комментарий

XVII — го века

Рассуждение о методе с Рене Декарта .

Первая страница « Геометрии » Рене Декарта.

XVII — го  века увидел сильное восстановление древних и исламская работ геометрии.

Есть три независимых прорыва, которые очень важны для коллективного подхода к нашему представлению пространственной реальности.

Рождение аналитической геометрии

Создание аналитической геометрии — это работа Декарта и, в меньшей степени, Ферма . Идеи Декарта — это система координат и ортогональная проекция . Эта теория позволяет представить геометрическое пространство как совокупность точек, каждая из которых представлена ​​тремя числами.

Декартово изобретение (1637 г.) представляет собой настоящую революцию в маленьком мире геометрии, поскольку благодаря использованию этих ориентиров эта наука в некотором смысле сводится к вычислениям на наборах из двух или трех чисел. Таким образом, древняя королева математики, которая была геометрией, была взята с престола в пользу науки, в конце концов, совершенно новой: алгебры.

Появление дифференциальных методов

Principia Mathematica — мастерская работа Ньютона, в которой он обновляет геометрическое видение Евклида, вводя дифференциальное исчисление.

Некоторые методы расчета Архимеда предполагали разделение элементов на все более мелкие. Например, чтобы приблизиться к пи, Архимед вычислил периметр многоугольника, описанного окружностью, и периметр вписанного многоугольника. Таким образом, он получил границу числа пи и этим методом нашел приближение 22/7.

В первой половине 17 века ряд западных ученых, таких как Ферма, Паскаль, Грегори , Барроу , Кавальери , хорошо знакомых с рассуждениями Архимеда, начали упрощать его методы.

Примерно в 1670-х годах выдающиеся английские и немецкие ученые Ньютон и Лейбниц наконец объяснили методы расчета, позволяющие использовать бесконечно малые величины. Это открытие — одно из самых важных, когда-либо сделанных в математике

Более того, это спровоцировало между двумя гениями, каждый из которых осознавал важность своего открытия, ссору, имеющую довольно серьезный приоритет … (учитывая явные различия в подходах к этому вопросу, сегодня это считается очень важным

пришел к тому же открытию независимо. На строгом календарном уровне приоритет открытия, по мнению его английских коллег, принадлежит Ньютону (публикация принадлежит Лейбницу).

Эти методы позволяют свести вычисление определенных геометрических характеристик изогнутых фигур, таких как углы между касательными, поверхностями и объемами, к вычислениям так называемых производных и интегралов (см. Статьи « Исчисление , производная и интегрирование (математика)» ). Они возвращают использование линейки и компаса к очень грубым инструментам, позволяя обрабатывать только очень конкретные фигуры.

Первые шаги проективной геометрии

Жирар Дезарг в иллюстрациях А. Боссе.

Еще одним оригинальным вкладом в XVII — го  века, в основном из — за Desargues , и в меньшей степени на Паскале , вдохновлена развитием геометрии работы по изучению конической точки зрения . Основное нововведение состоит во введении бесконечно удаленных точек в рассуждения о геометрии, помимо тех, которые используются для обоснования построений перспективного вида.

Среди обновленных свойств в этом контексте можно упомянуть теорему Дезарга и теорему Паскаля, чье потомство было удостоено Д. Гильберта .

Этот вклад будет идти довольно незаметно и его значение будет раскрыто в в XIX — м  века.

Примечания и ссылки

Заметки

1. Открытие таблички Плимптон 322 показывает, что теорема Пифагора, вероятно, была известна вавилонской цивилизации за 1000 лет до Пифагора.
2. Эта формула апокрифическая: ἀγεωμέτρητος μηδεὶς εἰσίτω — ageômetrètos mèdeis eisitô .
3. Две величины неизмеримы, если их соотношение не равно дроби. Также говорят, что это иррациональное число .
4. Геометрия не единственная дисциплина , чтобы увидеть ее развитие взрывается XVII — го  века. Мы увидим , об этой статье Математика в Европе в XVII — м  веке .
5. В том смысле, что нет причин приписывать неевклидовой геометрии онтологический статус, отличный от статуса евклидовой геометрии.

Рекомендации

1. «  da ich das der Geschrei Böotier scheue  » письмо Гаусса к Бесселю от 27 июня 1829 г., цитируемое в (de) H. Reichardt , Gauß und die nicht der Anfänge-euklidischen Geometry , Springer-Verlag ,2013, 250  с. , стр.  40.

Необычные свойства

Четырехугольник Ламберта в гиперболической геометрии

Четырехугольники Саккери в трех геометриях

Евклидова и неевклидова геометрии, естественно, обладают многими схожими свойствами, а именно теми, которые не зависят от природы параллелизма. Эта общность является предметом абсолютной геометрии (также называемой нейтральной геометрией )

Однако исторически наибольшее внимание уделялось свойствам, которые отличают одну геометрию от других.

Помимо поведения линий относительно общего перпендикуляра, упомянутого во введении, мы также имеем следующее:

• Ламберт четырехугольник является четырехугольник с тремя прямыми углами. Четвертый угол четырехугольника Ламберта острый, если геометрия гиперболическая, прямой угол, если геометрия евклидова, или тупой, если геометрия эллиптическая. Следовательно, прямоугольники существуют (утверждение, эквивалентное постулату параллельности) только в евклидовой геометрии.
• Саккрайте четырехугольник является четырехугольник с двух сторон равной длиной, и перпендикулярно к стороне называется база . Два других угла четырехугольника Саккери называются верхними углами, и они имеют одинаковую меру. Вершины четырехугольника Саккери острые, если геометрия гиперболическая, прямые углы, если геометрия евклидова, и тупые углы, если геометрия эллиптическая.
• Сумма углов любого треугольника меньше 180 °, если геометрия гиперболическая, равна 180 °, если геометрия евклидова, и больше 180 °, если геометрия эллиптическая. Дефект треугольника это числовое значение (180 ° — сумма мер углов треугольника). Этот результат можно также сформулировать так: дефект треугольников в гиперболической геометрии положительный, дефект треугольников в евклидовой геометрии равен нулю, а дефект треугольников в эллиптической геометрии отрицателен.

Важность

Перед тем была представлена Бельтрами, Клейном и Пуанкаром в модели неевклидовой плоскости, геометрия Евклида стояла неоспоримую как математическая модель в пространстве . Более того, поскольку суть предмета в синтетической геометрии была главным проявлением рациональности, евклидова точка зрения представляла абсолютный авторитет.

Открытие неевклидовой геометрии имело волновой эффект, выходящий далеко за рамки математики и естественных наук. Отношение философа Иммануила Канта к человеческому знанию сыграло особую роль в геометрии. Это был его главный пример синтетического априорного знания; не выведенные из органов чувств и не выведенные с помощью логики — наши знания о космосе были истиной, с которой мы родились. К несчастью для Канта, его концепция этой неизменно истинной геометрии была евклидовой. На богословие также повлиял переход от абсолютной истины к относительной истине в том, как математика соотносится с окружающим миром, что явилось результатом этой смены парадигмы.

Неевклидова геометрия является примером научной революции в истории науки , когда математики и ученые изменили свой взгляд на свои предметы. Некоторые геометры называли Лобачевского « Коперником геометрии» из-за революционного характера его работ.

Существование неевклидовой геометрии во многом повлияло на интеллектуальную жизнь виклидской Англии и, в частности, было одним из ведущих факторов, вызвавших пересмотр преподавания геометрии, основанного на Элементах Евклида . В то время этот вопрос об учебной программе горячо обсуждался и даже стал предметом книги « Евклид и его современные соперники» , написанной Чарльзом Латвиджем Доджсоном (1832–1898), более известным как Льюис Кэрролл , автором « Алисы в стране чудес» .

Подобные треугольники

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Треугольники АВС и A₁B₁C₁ будут подобны, если

∠ А = A₁, ∠ В = B₁, ∠ С = C₁,

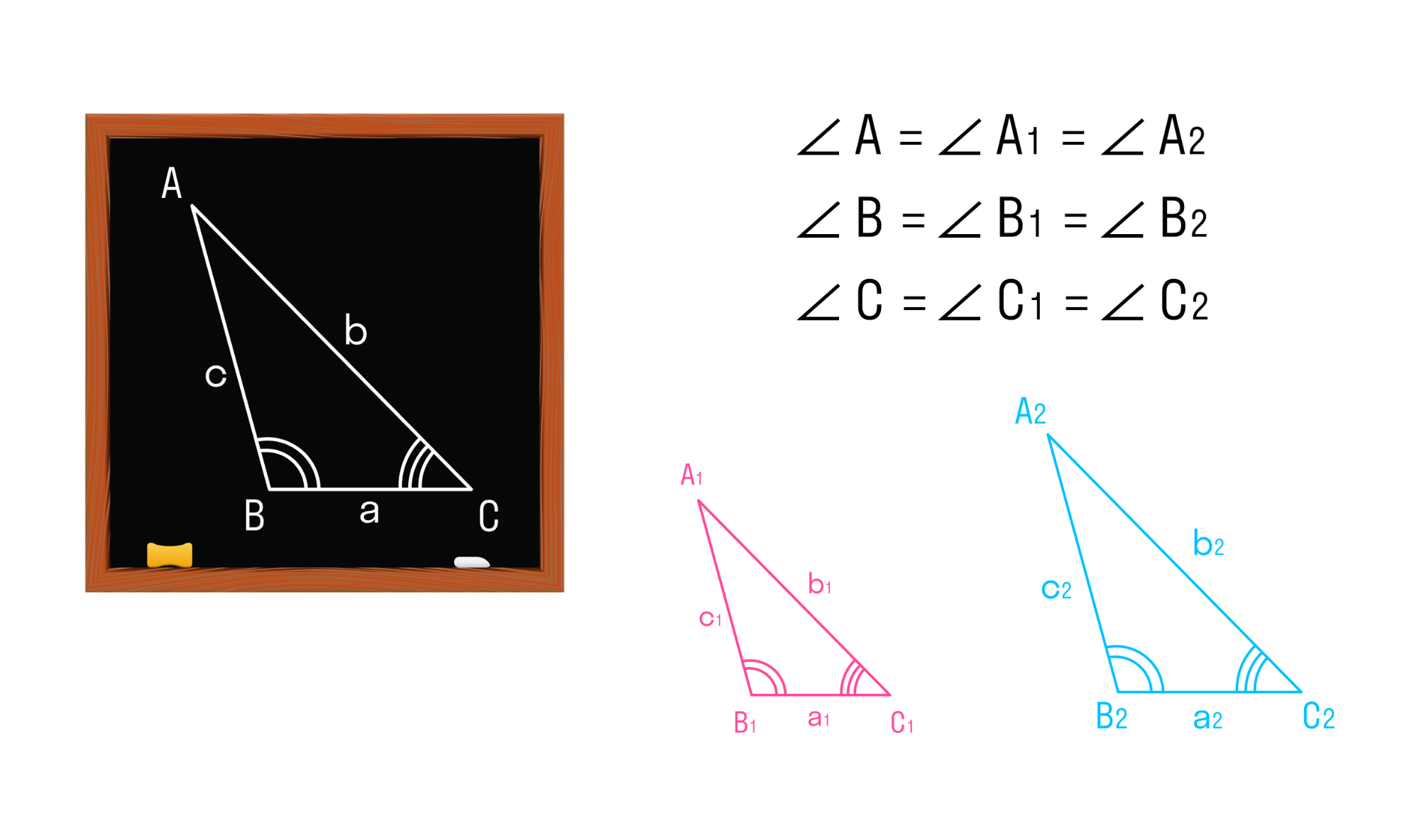
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A₁B₁C₁ подобны, это можно записать так: ΔАВС ∾ ΔA₁B₁C₁.

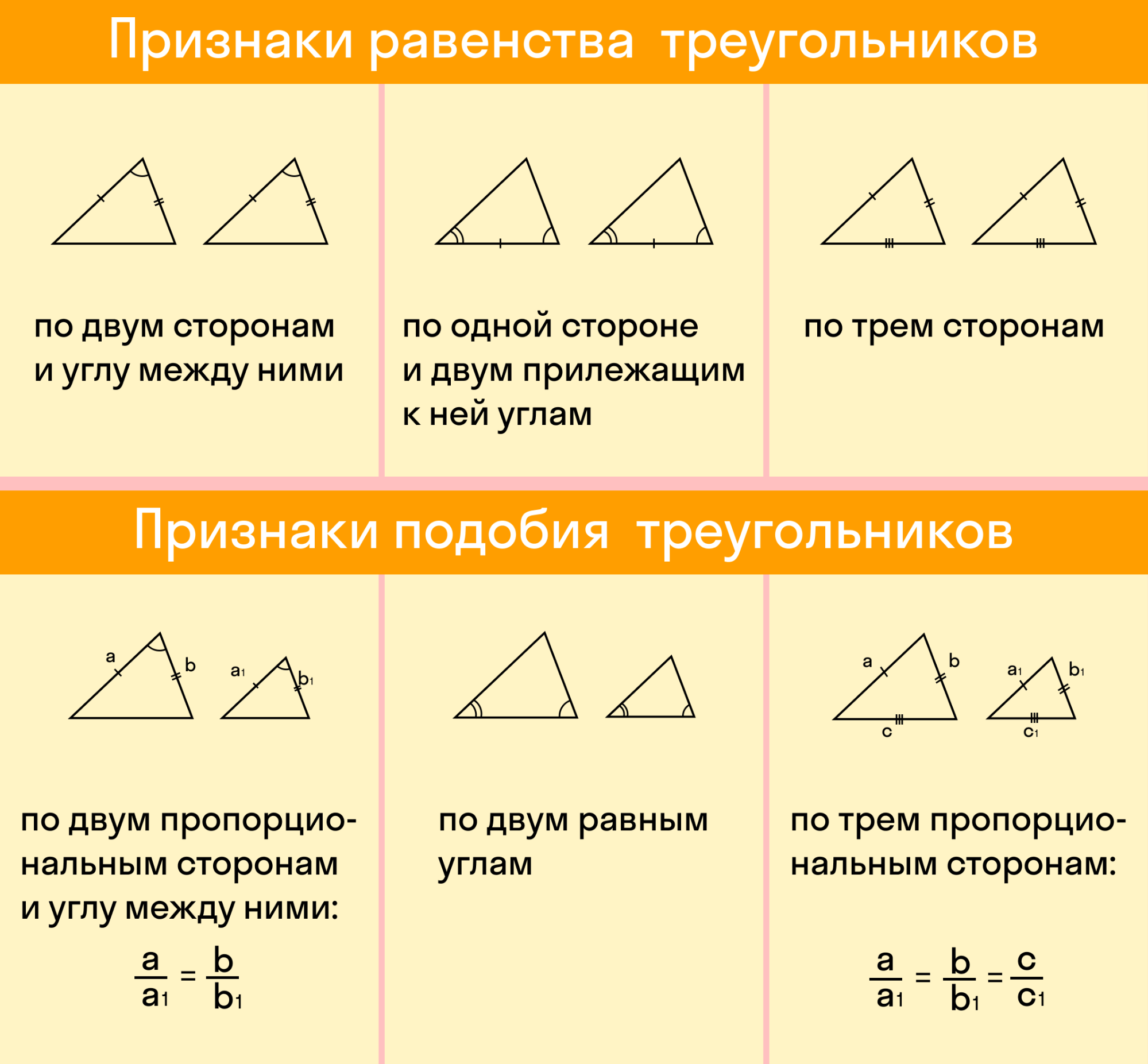
Теорема о первом признаке подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.

На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.

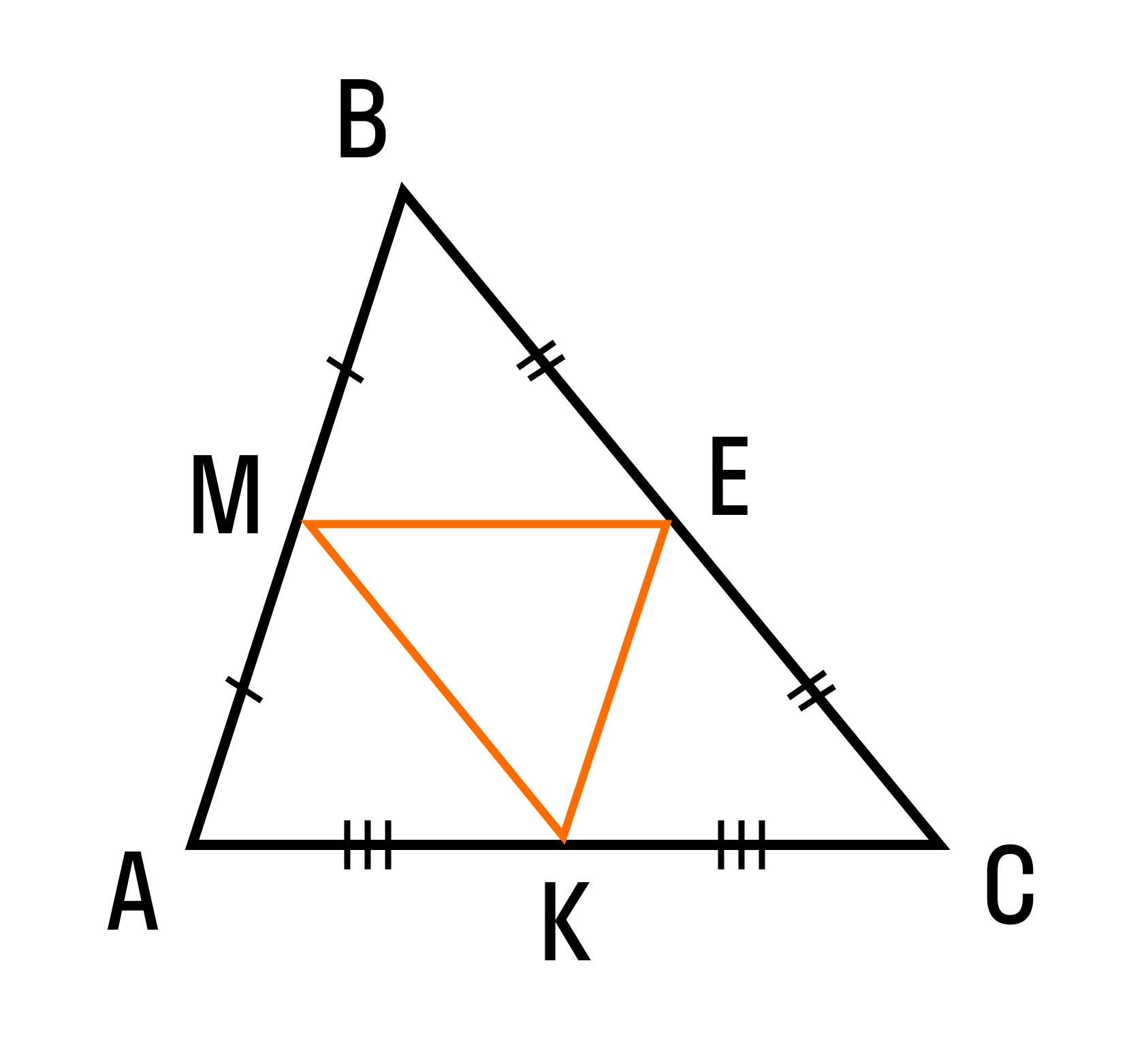
Теорема о средней линии звучит так:

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны

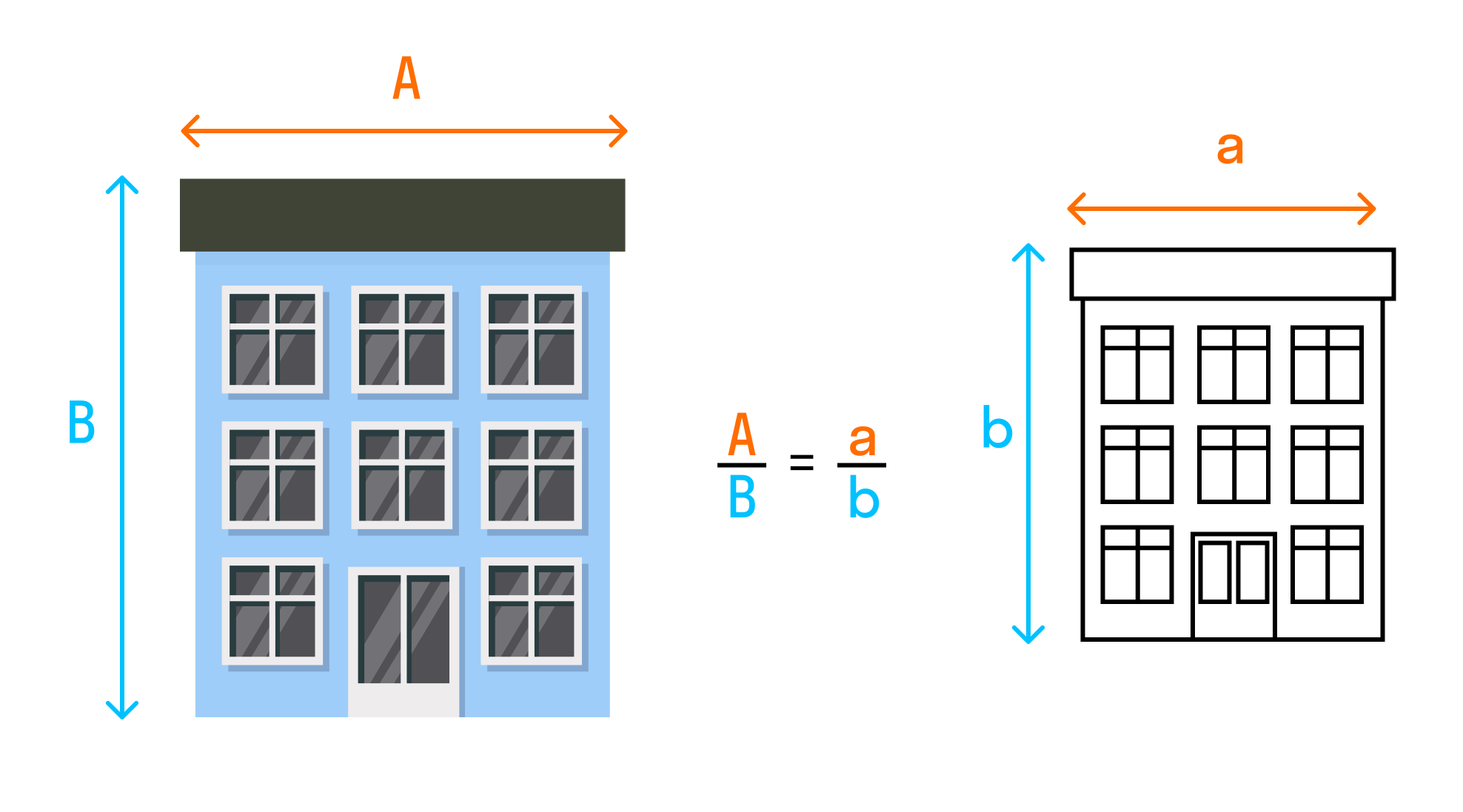
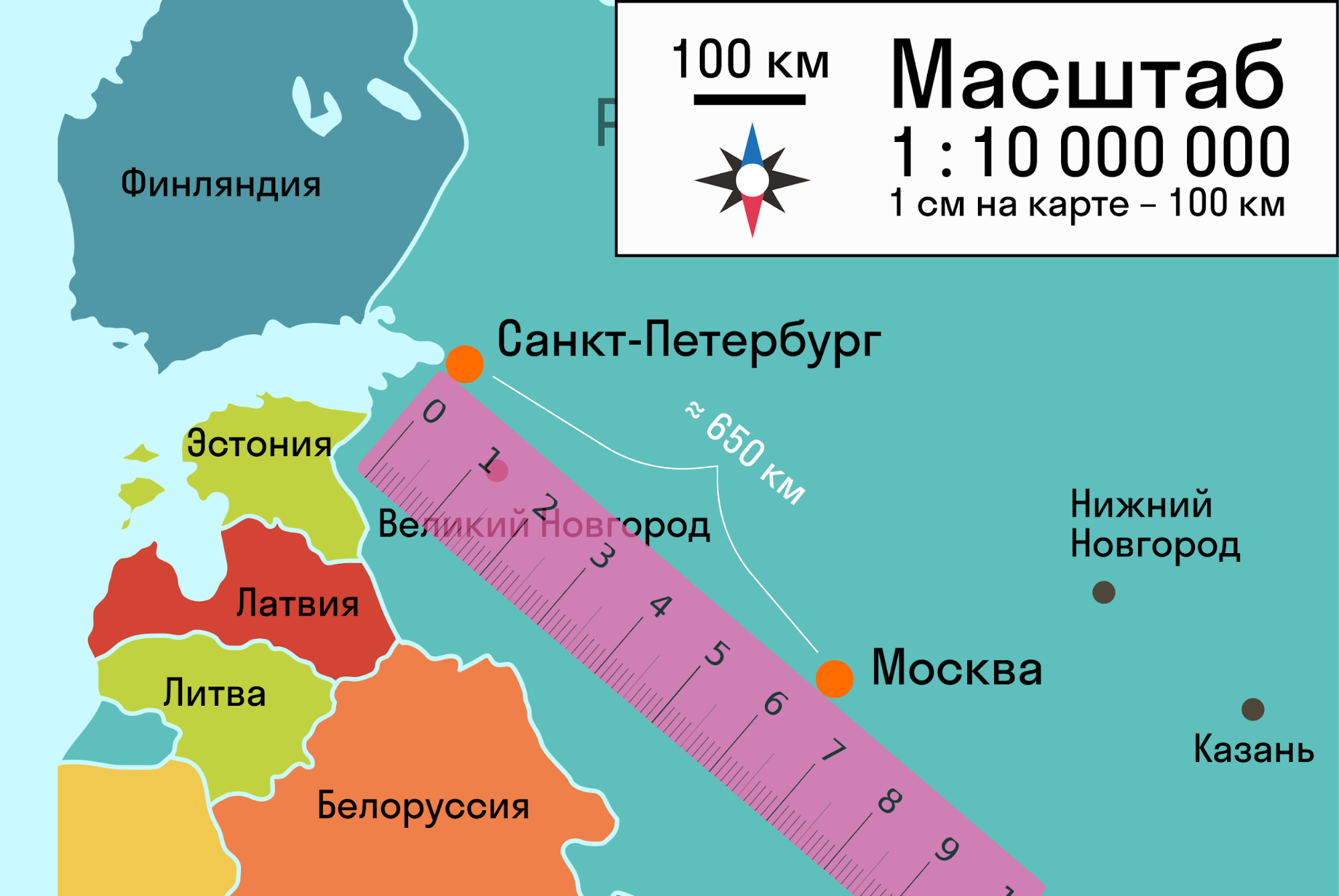
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.

Геометрия в природе

В окружающей действительности геометрия присутствует повсеместно. Природа щедро внедрила правильные геометрические формы практически во все свои творения. В затейливых узорах снежинок, составленных из многоугольников, отчетливо просматриваются шестиосные симметричные формы, объединенные общим центром.

Вообще, легкие зимние снежинки – это яркое воплощением красоты и порядка окружающей нас природы, на каждом шагу являющей примеры многообразия геометрических форм, объединенных принципом единства.

Распускающиеся нежные цветы и колючие ветвистые кустарники – при внимательном рассмотрении содержат в своей структуре правильные линии, взаимодействующие по геометрическим законам.

Архитектура и геометрия

Геометрические принципы внедрены во все проекты архитектурных сооружений. Неоспорима решающая роль геометрии при строительстве любых зданий.

Строительное проектирование всегда производится с учетом пространственных форм, влияющих на зрительное восприятие и относящихся к важнейшим характеристикам любого здания.

Геометрический вид, являющийся важным свойством сооружения и определяемый трехмерными размерами (ширина, глубина, высота), зависим от их соотношения. При равных размерах – форма архитектурного сооружения выглядит объемной, при одном из размеров значительно меньшем, чем два остальных – сооружение выглядит плоским, а в случае, когда два размера намного менее одного, сооружение приобретает линейный вид.

Архитектурные свойства определяются протяженностью по трем координатным осям и характеризуются размерами по высоте, ширине и глубине относительно размеров человека или смежных строений.

Модели неевклидовой геометрии

Сравнение эллиптической, евклидовой и гиперболической геометрий в двух измерениях

На сфере сумма углов треугольника не равна 180 °. Поверхность сферы не является евклидовым пространством, но локально законы евклидовой геометрии являются хорошими приближениями. В маленьком треугольнике на поверхности земли сумма углов очень близка к 180 °.

Двумерная евклидова геометрия моделируется нашим понятием «плоская плоскость ».

Эллиптическая геометрия

Простейшей моделью эллиптической геометрии является сфера, где линии представляют собой « большие круги » (например, экватор или меридианы на глобусе ), а точки, противоположные друг другу (называемые точками противоположностей ), идентифицируются (считаются одинаковыми). Это также одна из стандартных моделей реальной проективной плоскости . Разница в том, что в качестве модели эллиптической геометрии вводится метрика, позволяющая измерять длины и углы, а в качестве модели проективной плоскости такой метрики нет.

В эллиптической модели для любой данной прямой l и точки A , которая не находится на l , все прямые, проходящие через A, будут пересекать l .

Гиперболическая геометрия

Даже после работ Лобачевского, Гаусса и Бойяи оставался вопрос: «Существует ли такая модель для гиперболической геометрии ?». На модель гиперболической геометрии ответил Эудженио Бельтрами в 1868 году, который впервые показал, что поверхность, называемая псевдосферой, имеет соответствующую кривизну для моделирования части гиперболического пространства, а во второй статье того же года определил модель Клейна , которая моделирует целостность гиперболического пространства и использовал это, чтобы показать, что евклидова геометрия и гиперболическая геометрия были равносогласованными, так что гиперболическая геометрия была логически непротиворечивой тогда и только тогда, когда была евклидова геометрия. (Обратное утверждение следует из модели ориосферы евклидовой геометрии.)

В гиперболической модели внутри двумерной плоскости для любой данной прямой l и точки A , которая не находится на l , существует бесконечно много прямых, проходящих через A, которые не пересекаются с l .

В этих моделях концепции неевклидовой геометрии представлены евклидовыми объектами в евклидовой обстановке. Это приводит к искажению восприятия, при котором прямые линии неевклидовой геометрии представлены евклидовыми кривыми, которые визуально изгибаются. Этот «изгиб» не является свойством неевклидовых линий, а лишь искусственным способом их представления.

Трехмерная неевклидова геометрия

В трех измерениях есть восемь геометрических моделей. Как и в двумерном случае, существуют евклидова, эллиптическая и гиперболическая геометрии; смешанная геометрия, частично евклидова, частично гиперболическая или сферическая; витые варианты смешанной геометрии; и одна необычная геометрия, которая полностью анизотропна (т.е. каждое направление ведет себя по-разному).

Шаблоны для склеивания

Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.

Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.

Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.

Фигурок из треугольников

Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.

Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.

Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.

Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.

На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.

Основные ошибки при работе с моделями:

Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.

Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.

Оригами – бумажные фигурки, которые относятся к японскому искусству и существуют в нём уже не одно столетие. Монахи ещё в древние времена, использовали фигурки из бумаги для декорации храмов и его залов, а также для применения их в религиозных целях (осуществление обрядов).

Сделать оригами из бумаги своими руками в состоянии каждый малоопытный мастер, но главным критерием есть имение усидчивости и точности движений. Сегодня вы поймёте, что не нужно быть асом, чтобы красиво сделать эти изделия.

Геометрия и компьютерная графика

Компьютерная анимация (CGI) преображает сложные природные формы (такие, как лицо) в комплект несложных форм. Так, сложный объект создаётся за счет комбинации несложных объектов и может изменяться в следствии трансформации их геометрии. В базе данной идеи — изучения математиков, например, французско-американского ученого Бенуа Мандельброта, который в 1974 г. продемонстрировал, что естественные формы подчиняются правилам фрактальной размерности (неэвклидова геометрия), а в рамках классической евклидовой геометрии смогут быть измерены только примерно.

Компьютерная графика на основе фракталов Мандельброта

О том как знание математики позволяет заработать на майнинге криптовалюты.

Tags: «Начала» Евклида геометрия история математики

Средневековье и Возрождение

Сохранение древних произведений и латинские переводы греческих или арабских произведений являются основным вкладом западного средневековья в геометрию.

В целом средневековье в Западной Европе для геометрии, как и для многих других наук, было периодом упадка.

Геометрию, конечно, все еще преподают. Это часть квадривиума, который также включает арифметику , астрономию и музыку . Однако квадривиум гораздо менее популярен, чем тривиум ( грамматика , риторика и диалектика ): последний, вероятно, лучше подходит для общества, основным проектом которого является подготовка к пост-земной жизни.

В течение длительного периода , который тянется примерно с V — го  века XV — го  века ученые геодезистов редкость на Западе. Мы можем упомянуть Гербера д’Орийака, который стал папой под именем Сильвестра II, и особенно Леонардо Пизанского, известного как Фибоначчи; они по-прежнему более известны своей арифметической работой и страстью, с которой они переводили работы арабских ученых …

Возрождение к XV — го  века и XVI — го  века увидел первый тремор геометрической новости с появлением конической точки зрения которого теория подвергается нападению ряда ученых, в основном итальянцы, и самый известный, вероятно , Piero Франческа , Леонардо да Винчи , и Лука Пачоли , первые двое были обязаны своей славой больше своему художественному гению, чем математике.

Из истории геометрии

Подробности

Категория: Геометрия

Документальные учебные фильмы. Серия «Геометрия».

https://vk.com/video_ext.php

 Уже первобытные люди на самой начальной ступени своего развития должны были различать формы окружавших их предметов и замечать места их расположения. Так, они запоминали места охоты, места стоянок и селений. Они постепенно научились определять расстояния между отдельными предметами, размеры отдельных участков местности и т. п. По мере развития общественной жизни людей изучение форм и размеров предметов и их взаимного расположения становилось всё более нужным и требовало от человека всё больших знаний. В древнем Египте весенние разливы огромной реки Нила смывали границы между отдельными земельными участками. Нужно было ежегодно их восстанавливать, что было связано с большими измерительными работами на местности. Чтобы выполнять эти работы, надо было иметь удобные правила для вычисления длин линий, площадей, участков земли, для выполнения планировок местности и т. п. Эти правила были выработаны и записаны. Греки, ведя торговлю с египтянами, познакомились с этими правилами, дополнили их и постепенно развили из них целую науку, которую и назвали геометрией, что значит искусство измерять землю ( — земля, — измерять). Греческий учёный Евклид, живший в III в. до н. э., особенно подробно разработал эту науку и изложил её вместе с арифметикой в одиннадцати книгах, которые он назвал «Начала». По ним и изучали геометрию в последующие века. По образцу этих «Начал» составляются учебники геометрии и до нашего времени.Наблюдая окружающие нас предметы, мы замечаем большое разнообразие их внешнего вида и их свойств. Предметы отличаются один от другого своим видом, весом, свойствами вещества, из которого они состоят, и т. д. Но при всём этом разнообразии можно заметить свойство, присущее всем предметам без исключения, именно: каждый предмет имеет свою форму и свой размер. При изготовлении различных предметов им придают форму и размер, соответствующие их назначению. Артиллерийскому снаряду придают форму, при которой он имеет нужную дальность полёта, кузову корабля—форму, которая даёт ему устойчивое положение на поверхности воды и позволяет легче рассекать волны морской стихии. Далее, мы замечаем, что каждый предмет занимает определённое положение среди других предметов

В практической жизни весьма важно уметь определять расстояние между предметами, размещать их должным образом на нужных расстояниях. Так

на заводах весьма важно правильно расставить станки. На поле боя важно правильно разместить дзоты и наблюдательные пункты, уметь определить местонахождение огневых точек врага, расстояние до его блиндажей и т. п. Изучение форм и размеров предметов и их взаимного положения составляет отдельную область человеческого знания. Наука, изучающая формы, размеры и взаимное расположение предметов, называется геометрией.

 Геометрия, как и многие другие разделы математики, своими корнями уходит в «далекое прошлое. Слово «геометрия» в переводе с греческого означает «землемерие». ‘Такое название объясняется тем, что зарождение этого раздела математики было связано с различными измерительными работами, которые приходилась выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, геометрия возникла на основе практической деятельности людей и в начале своего развития служила в основном практическим целям. В дальнейшем геометрия сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур. Примеры геометрических фигур: треугольник, квадрат, окружность.

 Геометрические фигуры бывают весьма разнообразны. Часть любой геометрической фигуры является геометрической фигурой. Объединение нескольких геометрических фигур есть снова геометрическая фигура. На рисунке фигура слева состоит из треугольника и трех квадратов, а фигура справа состоит из окружности и частей окружности. Всякую геометрическую фигуру мы представляем себе составленной из точек.

Геометрия широко применяется на практике. Ее надо знать и рабочему, и инженеру, и архитектору, и художнику. Одним словом, геометрию надо знать всем.