233,евклид

Человек и его труд

«Начала» — самый влиятельный учебник из когда-либо созданных. Его продолжают издавать вот уже 2300 лет. Он дошел до настоящего времени благодаря Теону Александрийскому, издавшему «Начала» в своей редакции в IV в. н. э. «Началами» воодушевлялись такие ученые, как Коперник, Галилей, Ньютон и другие великие мыслители, поменявшие наш мир. О самом же Евклиде не известно ничего, не считая редких упоминаний о нем современников и утверждения Прокла (Прокл Диадох — античный философ V в. н. э.) в его «Комментариях к “Началам”» — только эти обрывочные сведения разрешают нам высказать предположение, что человек по имени Евклид действительно написал «Начала».

«Начала» Евклида – труд, переведённый на все языки мира в течение 23 веков, его издавали и копировали чаще всех прочих светских книг. На этой иллюстации – страницы «Начал», датируемые эпохой ренесанса.

Постулаты и аксиомы из трудов “Начала” Евклида

Многие теоремы, приведенные в «Началах», были сформулированы не Евклидом. Вклад Евклида заключался в том, дабы привести их к единому стандарту изложения и единому комплекту первоначальных предположений либо аксиом. В их число входят пять известных универсальных аксиом Евклида.

Геометрия

Универсальные аксиомы Евклида

1) величины, равные одному и тому же, равны и между собой;

2) если к равным величинам прибавляются равные, то и целые величины будут равны;

3) если от равных величин отнимаются равные, то остатки будут равны;

4) совмещающиеся (совпадающие) друг с другом величины равны между собой;

5) целое больше части.

Пять постулатов Евклида звучат более «геометрически»:

1) от всякой точки до всякой точки возможно провести участок прямой;

2) участок прямой возможно непрерывно продолжать по прямой;

3) из любой начальной точки участка прямой всяким радиусом может быть описана окружность, наряду с этим эта точка станет ее центром;

4) все прямые углы конгруэнтны (т. е. смогут быть преобразованы друг в друга);

5) если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов (равных 90°), то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов.

V постулат знаменит как постулат о параллельности. Позднее было доказано, что он недоказуем, что привело к появлению новых форм геометрии, основанных на другом комплекте аксиом.

Геометрия. Раздел математики

Раздел математики именуемый словом «геометрия» восходит к греческим «Земля» (гео) и «измерение» (метри). Как следует из названия данной дисциплины, грекам было нужно измерять элементарные природные формы. Практическое значение геометрии лежит в области землемерия и картографии, математических методов определения объема, площади и длины. Кроме этого, греческие ученые скоро поняли, что всякие формы подчиняются определенным закономерностям и правилам. Около 300 г. до н. э. греческий великий математик Евклид из Александрии собрал и детально обрисовал правила геометрии в труде «Начала», складывающемся из 13 книг. В нем он представил комплект определений, аксиом, теорем и математических доказательств, ставших основой геометрии как научной дисциплины. На изложенные в «Началах» положения опираются все математические дисциплины, развившиеся из геометрии. Вклад Евклида в математику настолько велик и глубок, что его называют «отцом геометрии».

Кинематическая геометрия

Гиперболическая геометрия нашла применение в кинематике с помощью физической космологии, введенной Германом Минковским в 1908 году. Минковский ввел такие термины, как мировая линия и собственное время, в математическую физику . Он понял, что подмногообразие событий в один момент собственного времени в будущем можно рассматривать как гиперболическое пространство трех измерений. Уже в 1890-х годах Александр Макфарлейн рисовал это подмногообразие с помощью своей « и гиперболических кватернионов , хотя Макфарлейн не использовал космологический язык, как Минковский в 1908 году. Соответствующая структура теперь называется гиперболоидной моделью гиперболической геометрии.

Неевклидовы плоские алгебры поддерживают кинематическую геометрию на плоскости. Например, разделенное комплексное число z = e a j может представлять пространственно-временное событие в один момент в будущем в системе отсчета с быстротой a . Кроме того, умножение на z равносильно преобразованию лоренцевского буста кадра с нулевой скоростью в кадр с быстротой а .

Кинематическое исследование использует двойственные числа для представления классического описания движения в абсолютном времени и пространстве : уравнения эквивалентны отображению сдвига в линейной алгебре:
zзнак равноИкс+уϵ,ϵ2знак равно,{\ displaystyle z = x + y \ epsilon, \ quad \ epsilon ^ {2} = 0,}Икс′знак равноИкс+vт,т′знак равнот{\ displaystyle x ^ {\ prime} = x + vt, \ quad t ^ {\ prime} = t}

(Икс′т′)знак равно(1v1)(Икст).{\ displaystyle {\ begin {pmatrix} x ‘\\ t’ \ end {pmatrix}} = {\ begin {pmatrix} 1 & v \\ 0 & 1 \ end {pmatrix}} {\ begin {pmatrix} x \\ t \ end {pmatrix}}.}

С двойными числами отображение т′+Икс′ϵзнак равно(1+vϵ)(т+Иксϵ)знак равнот+(Икс+vт)ϵ.{\ displaystyle t ^ {\ prime} + x ^ {\ prime} \ epsilon = (1 + v \ epsilon) (t + x \ epsilon) = t + (x + vt) \ epsilon.}

Другой взгляд на специальную теорию относительности как на неевклидову геометрию был предложен Э.Б. Уилсоном и Гилбертом Льюисом в Трудах Американской академии искусств и наук в 1912 году. Они переработали аналитическую геометрию, заложенную в алгебре расщепленных комплексных чисел, в синтетическую геометрию предпосылок. и отчисления.

Вариации и обобщения

Если в качестве основного поля использовать не поле вещественных чисел, а поле комплексных, то это даст определение унитарного (или эрмитова) пространства.

Отказ от требования конечномерности даёт определение предгильбертова пространства. Отказ от требования положительной определённости скалярного произведения приводит к определению псевдоевклидова пространства. Требование того, чтобы предгильбертово пространство было полным по метрике, ведёт к определению гильбертова пространства; пространство квадратично-суммируемых последовательностей — гильбертово пространство, которое может рассматриваться как пространство векторов с бесконечным числом координат.

Интересные факты из жизни

Несколько любопытных фактов из биографии Евклида:

1. Самый древний известный математический трактат принадлежит Евклиду.
2. До сих пор нет данных о месте рождения и смерти великого ученого. Однако известно место занятий Евклида примерно 2400 лет назад и место его нахождения — Александрия. Интересно, что этот городок сегодня — второй по размерам в Египте после Каира;
3. Евклид смог создать 4 книжки по коническому виду сечений.
4. Фундаментальный труд «Начала» считается настолько важным для науки, что до сих пор его используют в жизни. Интересно, что есть другие публикации с подобным наименованием, но самый популярный — труд Евклида».
5. С самой юности Евклид обучался у именитого ученого Платона, обучавшего Аристотеля в Древней Греции. Сам же Платон обучался у Сократа.
6. По традиции геометрия сегодня носит название этого ученого.
7. Есть легенда, что когда один раз ученик величайшего математика спросил у него, как геометрия может помочь ему в жизни, то Евклид дал ему денег и прогнал с занятий.
8. Евклид до сих пор считается автором многочисленных книг, чье авторство не было подтверждено. Это разные труды, к примеру, публикации по музыке, философии и медицине. Официально известно, что великий ученый сделал открытие в оптических и астрономических областях.
9. Сегодня признают римановскую, лобачевскую и евклидову геометрию. Последняя — самая традиционная и часто используемая.
10. В первый раз евклидовский труд перевели в конце восемнадцатого века. При этом «Начала» впервые были переведены на армянский язык в одиннадцатом веке.
11. Любимая фраза: «Нет царского пути в геометрии».

В целом, Евклид является отцом геометрии, и он не случайно так называется. Он первым сделал сложное понятным и дал толчок развитию естественных наук. Его книги неоценимы по значимости и применяются сегодня в области математических и геометрических наук во всем мире.

Постулаты Евклида

Его главная книга «Элементы» (первоначально написанная на древнегреческом языке) стала базовой работой важных математических учений. Она разделена на 13 отдельных книг.

• Книги от первой до шестой посвящены геометрии плоскости.
• Книги семь-девять имеют дело с теорией чисел
• Книга восьмая о геометрической прогрессии
• Книга десятая посвящена иррациональным числам
• Книги одиннадцать-тринадцать представляют собой трехмерную геометрию (стереометрию).

Гений Евклида состоял в том, чтобы взять в оборот множество разнообразных элементов математических идей и объединить их в один логический, последовательный формат.

Лемма Евклида, которая утверждает, что фундаментальное свойство простых чисел состоит в том, что если простое число делит произведение двух чисел, оно должно делить по крайней мере одно из этих чисел.

Что такое «евклидова геометрия»?

Свои знания в планиметрии и стереометрии гениальный мыслитель формулировал в виде аксиом и постулатов. Система аксиом касалась четырёх понятий: точки, прямой, плоскости, движения, а также взаимоотношения этих понятий между собой.

Для построения конкретных фигур на плоскости или в пространстве он разработал систему постулатов, предписывающих конкретные действия. Подобная система аксиом и постулатов в современности получила название «евклидова геометрия».

Аксиоматическая основа неевклидовой геометрии

Евклидова геометрия может быть описана аксиоматически несколькими способами. К сожалению, первоначальная система пяти постулатов (аксиом) Евклида не входит в их число, так как его доказательства опирались на несколько неустановленных предположений, которые также следовало принять в качестве аксиом. Система Гильберта, состоящая из 20 аксиом, наиболее точно следует подходу Евклида и обеспечивает обоснование всех доказательств Евклида. Другие системы, использующие разные наборы неопределенных терминов, получают ту же геометрию разными путями. Однако все подходы имеют аксиому, которая логически эквивалентна пятому постулату Евклида, постулату параллельности. Гильберт использует форму аксиомы Плейфэра, в то время как Биркгоф , например, использует аксиому, которая гласит: «Существует пара похожих, но не совпадающих треугольников». В любой из этих систем удаление одной аксиомы, эквивалентной постулату параллельности, в какой бы форме она ни принималась, и оставление всех остальных аксиом нетронутыми, дает абсолютную геометрию . Поскольку первые 28 утверждений Евклида (в «Элементах» ) не требуют использования постулата параллельности или чего-либо эквивалентного ему, все они являются истинными утверждениями в абсолютной геометрии.

Чтобы получить неевклидову геометрию, постулат параллельности (или его эквивалент) должен быть заменен его отрицанием . Отрицание формы аксиомы Playfair , поскольку это составное утверждение (… существует один и только один …), можно сделать двумя способами:

• Либо будет существовать более одной прямой, проходящей через точку, параллельную данной прямой, либо не будет никаких прямых, проходящих через точку, параллельную данной прямой. В первом случае, заменяя постулат параллельности (или его эквивалент) утверждением «В плоскости, для данной точки P и прямой l, не проходящей через P, существуют две прямые, проходящие через P, которые не пересекаются с l » и сохраняя все остальные аксиомы дают гиперболическую геометрию .
• Со вторым случаем справиться не так просто. Простая замена постулата параллельности утверждением: «В плоскости, если дана точка P и прямая l, не проходящая через P, все прямые, проходящие через P, пересекаются с l », не дает согласованного набора аксиом. Это следует из того, что параллельные прямые существуют в абсолютной геометрии, но это утверждение говорит об отсутствии параллельных прямых. Эта проблема была известна (в ином виде) Хайяму, Саккери и Ламберту и послужила основанием для их отказа от так называемого «случая тупого угла». Чтобы получить непротиворечивый набор аксиом, включающий эту аксиому об отсутствии параллельных прямых, необходимо изменить некоторые другие аксиомы. Эти корректировки зависят от используемой системы аксиом. Среди прочего, эти настройки имеют эффект модификации второго постулата Евклида от утверждения, что отрезки линии могут быть неограниченно продолжены, до утверждения, что линии не ограничены. Римана «с эллиптической геометрией возникает как наиболее естественной геометрии , удовлетворяющей эту аксиому.

Геометрия Евклида

В самом узком смысле евклидова геометрия — это геометрия, которую Евклид представил в «Элементах» .

Геометрия (персонификация) учит в евклидовой геометрии. (Иллюстрация начала XIV века)

В соответствии с этой аксиоматической структурой более двух тысяч лет преподавалась геометрия. Фраза «more geometryo» (лат. «В манере (евклидовой) геометрии») до сих пор служит ссылкой на строго дедуктивную аргументацию.

Евклид делает это следующим образом:

Определения

Книга начинается с нескольких определений , например:

• Один момент — это то, что не имеет частей.
• Линия является длина без ширины.
• Прямая линия , которая всегда одинакова по отношению к точкам на ней.

Точно так же плоскости , углы и т. Д. Определяются.

В дополнение к этим более или менее четким определениям основных терминов, существуют также определения, которые следует понимать как введение слов в современном смысле , потому что они используются в сокращенной форме в следующем тексте, например, для параллелей : «Параллельные являются прямые линии, лежащие в одной плоскости и в одно и то же время, если они продолжаются до бесконечности с обеих сторон, они не пересекаются с обеих сторон ».

Элементы дают в общей сложности 35 определений.

Постулаты

После более описательных определений следуют еще пять определяющих постулатов . Здесь требуется

• что можно проложить маршрут из любой точки в любую точку,
• что ограниченная прямая линия может быть продолжена непрерывно,
• что вы можете нарисовать круг с любым центром и расстоянием ,
• что все прямые углы равны друг другу и
• что если бы прямая линия при пересечении с двумя прямыми имела эффект, заключающийся в том, что углы, созданные внутри на одной стороне, были бы меньше двух прямых, тогда две прямые линии встретились бы на той стороне, на которой лежат углы, когда они продолжены до бесконечности, которые вместе меньше двух правильных (короче: для прямой линии, проходящей через данную точку, которая будет лежать вне этой прямой, может существовать не более одной прямой, параллельной ей, см. постулат параллелей ).

Аксиомы евклида

• То, что одинаково, равно одно другому.
• Если подобное добавляется к подобному, то суммы одинаковы.
• Если подобное отделяется от подобного, то остается то же самое.
• Что можно сделать совпадающим друг с другом, равно друг другу.
• Целое больше, чем часть.

Проблемы и теоремы

Основываясь на этом, Евклид теперь решает проблемы …

Пример : «Постройте равносторонний треугольник над заданным маршрутом».

… и теоремы

Пример : «Если в треугольнике два угла равны, стороны, противоположные этим углам, также должны быть равны друг другу».

Для решения проблемы или доказательства теоремы в основном используются только определения, постулаты и аксиомы, а также ранее доказанные теоремы и конструкции из ранее решенных задач.

Геометрия и реальность в Евклиде

Как платоник Евклид был убежден, что сформулированные им постулаты и аксиомы отражают реальность. Согласно теории идей Платона , они принадлежат к онтологически более высокому уровню, чем нарисованные на песке фигуры, являющиеся их изображениями. Отношения между неидеально нарисованным кругом и идеальной идеей круга иллюстрируют разницу между чувственно воспринимаемым миром и умопостигаемым (только духовно воспринимаемым) миром, что проиллюстрировано платоновской аллегорией пещеры .

Отличия от чисто аксиоматической теории

С сегодняшней точки зрения, элементы не соответствуют требованиям аксиоматической теории :

• Цель определений (поскольку они касаются основных терминов) в случае Евклида — установить ссылку на знакомый геометрический мир опыта и мотивировать постулаты. О выразительности таких предложений судят по-разному. Строгие аксиомы считают их излишними.
• Пять постулатов наиболее точно представляют то, что сегодня считалось бы аксиомой . Однако они недостаточно полны и слишком неточны в качестве основы для выводов, сделанных на их основе. — Следует отметить, что по крайней мере первые три «постулата» постулируют возможность определенных построений (а не правильность определенных фактов). Поэтому аксиоматику Евклида можно также назвать конструктивной аксиоматикой.
• Утверждения, называемые аксиомами, относятся не столько к геометрии, сколько к логической основе. Однако с точки зрения логического обоснования они неполны.

Отсюда следует, что в умозаключениях неизбежно используются различные невысказанные предположения.

Краткая биография

Биография Евклида до конца не изучена, к примеру, до сих пор неизвестен год рождения. Известно, что он появился на свет в небольшом районе Афин и был платоновским учеником.

Подъем его научной работы пришелся на правление Птолемея Первого. Некоторые сведения о его жизни можно проследить по арабским рукописям и архимедовым письмам к друзьям. Так, по ним можно определить, что Евклид был сыном греческого ученого и жил около Тира в Сирии.

С малых лет получал знания о мире от своего отца, он же привил сыну любовь к естественным наукам, а затем Евклид поступил в школу Платона, где и обучился математическим основам.

Повзрослев, его пригласили в храм Мусейон (по другим данным он был одним из его основателей), в котором собирались видные ученые с поэтами. Тут были классы для занятий. Также храм был заполнен садами с башнями астрономии, помещениями для одиноких размышлений и большой библиотекой.

В Мусейоне он смог открыть школу с лучшими математиками и монументальный труд в области математики, в котором заложил планиметрические основы со стереометрией, теорией чисел, законами алгебры, методами нахождения площадей с объемами и др.

Фрагмент папируса с текстом «Начал» Евклида

Монументальный труд — публикация «Начала». Это серия из 13 книг, представляющая собой обработанные публикации древнегреческих математиков с пятого по четвертый век до нашей эры.

Кроме «Начал», было создано еще одно сочинение — «Данные», в котором были опубликованы основы по геометрическому анализу. Кроме того, александрийский ученый создал учебник, с помощью которого в то время и сейчас изучают астрономию, перспективу, отражение в зеркале, музыкальные интервалы и решают тригонометрические задачи.

Все оставшиеся годы жизни посвятил изучению естественных наук и математических законов, отчего его называют отцом геометрии. О других аспектах его жизни неизвестно до сих пор. Умер в Александрии.

Это интересно: 231,ДУХОВНАЯ КУЛЬТУРА — разбираемся внимательно

Обзор

Размерность

Число степеней свободы для E ( n ) равно n ( n + 1) / 2 , что дает 3 в случае n = 2 и 6 для n = 3 . Из них n можно отнести к имеющейся трансляционной симметрии , а оставшиеся n ( n — 1) / 2 — к вращательной симметрии .

Прямая и косвенная изометрии

Прямые изометрии (то есть изометрии , сохраняющая беспристрастность из хиральных подмножеств) содержать подгруппу Е ( п ), называются специальной евклидовой группа и обычно обозначаются через Е + ( п ) или SE ( п ). Они включают переводы и вращения, а также их комбинации; включая преобразование идентичности, но исключая любые отражения.

Изометрии обратной руки называются косвенными или противоположными . Для любой фиксированной косвенной изометрии R , такой как отражение относительно некоторой гиперплоскости, любая другая косвенная изометрия может быть получена путем композиции R с некоторой прямой изометрией. Следовательно, косвенные изометрии являются смежным классом E + ( n ), который можно обозначить E — ( n ). Отсюда следует, что подгруппа E + ( n ) имеет индекс 2 в E ( n ).

Топология группы

Естественная топология евклидова пространства влечет топологию евклидовой группы E ( n ). А именно, последовательность f _i изометрий ( i ∈ ) определяется как сходящаяся тогда и только тогда, когда для любой точки p из последовательность точек p _i сходится.
Eп{\ displaystyle \ mathbb {E} ^ {n}}Eп{\ displaystyle \ mathbb {E} ^ {n}}N{\ Displaystyle \ mathbb {N}}Eп{\ displaystyle \ mathbb {E} ^ {n}}

Из этого определения следует, что функция непрерывна тогда и только тогда, когда для любой точки p из функция, определяемая формулой f _p ( t ) = ( f (t)) ( p ), является непрерывной. Такая функция называется «непрерывной траекторией» в E ( n ).
ж,1→E(п){\ displaystyle f: \ rightarrow E (n)}Eп{\ displaystyle \ mathbb {E} ^ {n}}жп,1→Eп{\ displaystyle f_ {p}: \ rightarrow \ mathbb {E} ^ {n}}

Оказывается, специальная евклидова группа SE ( n ) = E + ( n ) связна в этой топологии. То есть, учитывая любые два прямых изометрии A и B из , существует непрерывная траектория F в E + ( п ) такая , что F (0) = и F (1) = B . То же верно и для непрямых изометрий E — ( n ). С другой стороны, группа E ( n ) в целом не связна: не существует непрерывной траектории, которая начинается в E + ( n ) и заканчивается в E — ( n ).
Eп{\ displaystyle \ mathbb {E} ^ {n}}

Непрерывные траектории в E (3) играют важную роль в классической механике , поскольку они описывают физически возможные движения твердого тела в трехмерном пространстве во времени. Берут е (0) , чтобы быть тождественное преобразование я из , который описывает начальное положение тела. Положение и ориентация тела в любой более поздний момент времени t будет описываться преобразованием f (t). Поскольку f (0) = I находится в E + (3), то же самое должно относиться к f (t) в любое более позднее время. По этой причине прямые евклидовы изометрии также называют «жесткими движениями».
E3{\ displaystyle \ mathbb {E} ^ {3}}

Структура лжи

Евклидовы группы — это не только топологические группы , но и группы Ли , так что понятия исчисления могут быть немедленно адаптированы к этой ситуации.

Отношение к аффинной группе

Евклидова группа E ( n ) является подгруппой аффинной группы для n измерений и таким образом, чтобы уважать структуру полупрямого произведения обеих групп. Это дает, a fortiori , два способа записи элементов в явной нотации. Эти:

1. с помощью пары ( A , B ) , с А п × п ортогональной матрицы , а б реального вектор — столбец размера п ; или же
2. единственной квадратной матрицей размера n + 1 , как объяснено для аффинной группы .

Подробности первого представления приведены в следующем разделе.

В терминах Феликс Клейн «s программы Эрлангена , мы считывать из этого , что евклидовой геометрии , геометрия Евклида группы симметрий, является, следовательно, специализацией аффинной геометрии . Применяются все аффинные теоремы. Происхождение евклидовой геометрии позволяет определить понятие расстояния , из которого затем можно вывести угол .

[править] Система измерения и арифметики

Евклидова геометрия имеет два основных типа измерений: угол и расстояние. Угловая шкала является абсолютной, и Евклид использует прямой угол в качестве своей основной единицы, так что, например, угол в 45 градусов будет называться половиной прямого угла. Шкала расстояний относительна; один произвольно выбирает отрезок прямой с некоторой ненулевой длиной в качестве единицы, а другие расстояния выражаются относительно него. Сложение расстояний представлено конструкцией, в которой один линейный сегмент копируется на конец другого линейного сегмента для увеличения его длины, и аналогично для вычитания.

Измерения площади и объема производятся на основе расстояний. Например, прямоугольник шириной 3 и длиной 4 имеет площадь, представляющую произведение, 12. Поскольку эта геометрическая интерпретация умножения была ограничена тремя измерениями, не существовало прямого способа интерпретации произведения четырех или более чисел, и Евклид избегал таких произведений, хотя они подразумеваются, например, в доказательстве книги IX, предложение 20.

Евклид называет пару линий, пару плоских или твердых фигур «равными» (ἴσος), если их длина, площадь или объем равны соответственно, и аналогично для углов. Более сильный термин «конгруэнтный» относится к идее, что вся фигура имеет тот же размер и форму, что и другая фигура. В качестве альтернативы, две фигуры являются конгруэнтными, если одну можно поставить поверх другой, чтобы она точно совпала с ней (gереворачивание разрешено.) Таким образом, например, прямоугольник 2×6 и прямоугольник 3×4 равны, но не конгруэнтны, а буква R конгруэнтна своему зеркальному отображению. Фигуры, которые были бы совпадающими, за исключением различий в размерах, называются подобными. Соответствующие углы в паре одинаковых форм конгруэнтны, а соответствующие стороны пропорциональны друг другу.

Линейная оболочка

Линейной оболочкой L(X) подмножества X линейного пространства V называется совокупность всевозможных линейных комбинаций элементов из X,

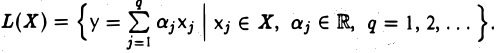
Последнее читается так: «линейная оболочка L(X) состоит из всевозможных элементов у, представимых в виде линейных комбинаций элементов множества X».

Основные свойства линейной оболочки

1. Линейная оболочка L(X) содержит само множество X.
2. L(X) — линейное подпространство пространства V.

Сумма линейных комбинаций элементов множества X и произведение линейной комбинации элементов на любое число снова являются линейными комбинациями элементов множества X.

3. L(X) — наименьшее линейное подпространство, содержащее множество X.

Это свойство следует понимать так: если линейное подпространство W содержит множество X , то W содержит и его линейную оболочку L(X).

Пусть W — линейное подпространство, содержащее заданное множество X. Тогда произвольная линейная комбинация элементов множества X — элемент линейной оболочки L(X) — содержится и в подпространстве W.

Пример:

Рассмотрим в линейном пространстве R3 две тройки ξ = (1,1,0) и η = (1,0, I) (рис.4). Множество решений уравнения

является линейной оболочкой L(ξ , η) троек ξ и η. Действительно, тройки (I, 1, 0) и (1, 0, I) образуют фундаментальную систему решений однородного уравнения (2), и значит, любое решение этого уравнения является их линейной комбинацией.

Пример:

Рассмотрим в линейном пространстве С(- ∞, ∞) вещественнозначных функций, непрерывных на всей числовой оси, набор X одночленов 1, х,…, хn:

Линейная оболочка L(X) представляет собой совокупность многочленов с вещественными коэффициентами, степени которых не превосходят n.

Обозначение:

Тексты и переводы

Старые русские переводы

• Эвклидовы элементы из двенадцати нефтоновых книг выбранные и в осмь книг чрез профессора мафематики А. Фархварсона сокращённые. / Пер. с лат. И. Сатарова. СПб., 1739. 284 стр.
• Елементы геометрии, то есть первые основания науки о измерении протяжении, состоящие из осьми Евклидовых книг. / Пер. с франц. Н. Курганова. СПб., 1769. 288 стр.
• Евклидовых стихий осьмь книг, а именно: 1-я, 2-я, 3-я, 4-я, 5-я, 6-я, 11-я и 12-я. / Пер. с греч. СПб., 1784

  2-е изд. … к сим прилагаются книги 13-я и 14-я. 1789. 424 стр.

  . 370 стр.

• Эвклидовых начал три книги, а именно: 7-я, 8-я и 9-я, содержащие общую теорию чисел древних геометров. / Пер. Ф. Петрушевского. СПб., 1835. 160 стр.
• Восемь книг геометрии Эвклида. / Пер. с нем. воспитанниками реального училища… Кременчуг, 1877. 172 стр.
• Начала Евклида. / С введ. и толкованиями М. Е. Ващенко-Захарченко. Киев, 1880. XVI, 749 стр.

Средневековые армянские переводы

В XI веке Григор Магистрос перевел с греческого на армянский «Начала» Евклида. Более обширный перевод Евклида сделан в позднем средневековье и приписывается автору XVII века Григору Кесараци.

Современные издания сочинений Евклида

Начала Евклида. Пер. и комм. Д. Д. Мордухай-Болтовского при ред. участии И. Н. Веселовского и М. Я. Выгодского. В 3 т. (Серия «Классики естествознания»). М.: ГТТИ, 1948-50. 6000 экз.

• Евклидов корпус. Деление канона. Перевод А. Щетникова. ΣΧΟΛΗ, 6, 2012, c. 98-110.
• Евклид. Оптика. Перевод А. Щетникова. ΣΧΟΛΗ, 13, 2019, c. 771—822.
• Euclidus Opera Omnia. Ed. I. L. Heiberg & H. Menge. 9 vols. Leipzig: Teubner, 1883—1916.

• Euclide. Les éléments. 4 vols. Trad. et comm. B. Vitrac; intr. M. Caveing. P.: Presses universitaires de France, 1990—2001.
• Barbera A. The Euclidian Division of the Canon: Greek and Latin Sources // Greek and Latin Music Theory. Vol. 8. Lincoln: University of Nebraska Press, 1991.